Duration
Duration is the time it takes for an investor to be repaid the price for a bond by the bond's total cash flows.For example, suppose the current price of a bond is $970, maturity is in three years, the annual coupon payment is $50, and the current market interest rate is 7%. The present worth of the coupon payments and payment of the $1,000 principal is $2,686.23. The duration, calculated by dividing the present worth by the current price is:
$2,686.23 / $970 = 2.77 years
Bonds that pay coupon interest will always have a duration less than maturity. Zero coupon bonds, with no coupon payments, have a duration equal to maturity.
Using duration, it's possible to approximate how much a bond's price is likely to rise or fall when interest rates change. As interest rates increase, a bond's price decreases.
Duration measures how quickly a bond will repay its price. The longer it takes, the greater exposure the bond has to changes in the interest rate environment. Therefore, the longer the duration, the higher is the interest rate risk (as opposed to default risk).
Here are some of factors that affect a bond's duration:
- Time to maturity: Consider two bonds that each cost $1,000 and yield 5%. A bond that matures in one year would more quickly repay its true cost than a bond that matures in 10 years. As a result, the shorter-maturity bond would have a lower duration and less risk. The longer the maturity, the higher the duration, and the greater the interest rate risk.
- Coupon rate: A bond's payment is a key factor in calculating duration. If two otherwise identical bonds pay different coupons, the bond with the higher coupon will pay back its original cost quicker than the lower-yielding bond. The higher the coupon, the lower the duration, and the lower the interest rate risk.
Knowing the duration of a bond, or a portfolio of bonds, gives an investor an advantage in two important ways:
- Speculating on interest rates: Investors who anticipate a decline in market interest rates, as a result of, for instance, a stimulative rate cut by the Federal Reserve, would try to increase the average duration of their bond portfolio. Likewise, investors who expect the Fed to raise interest rates would want to lower their average duration.
- Matching bond selection to your risk: When selecting from bonds of different maturities and yields, duration allows you to quickly determine which bonds are more sensitive to changes in market interest rates, and to what degree.
Duration Verses Maturity
Bond prices change inversely with interest rates, and, hence, there is interest rate risk with bonds. One method of measuring interest rate risk is by the full valuation approach, which simply calculates what bond prices will be if the interest rate rose by specific amounts. The full valuation approach is based on the fact that the price of a bond is equal to sum of the present value of each coupon payment plus the present value of the principal payment.
Bond Value = Present Value of Coupon Payments + Present Value of Par Value
Another method, which is less computationally intensive, is by calculating the duration of a bond, which is the weighted average of the present value of the bond’s payments, and can be viewed as the average, or effective, maturity of a bond. Graphically, the duration of a bond can be envisioned as a seesaw where the fulcrum is placed so as to balance the weights of the present values of the payments and the principal payment. The longer the duration, the longer is the average maturity, and, therefore, the greater the sensitivity to interest rate changes.
Although the effective duration is measured in years, it is more useful to interpret duration as a means of comparing the interest rate risks of different securities. Securities with the same duration have the same interest rate risk exposure. For instance, since zero-coupon bonds only pay the face value at maturity, the duration of a zero is equal to its maturity. It also follows that any bond of a certain duration will have an interest rate sensitivity equal to a zero-coupon bond with a maturity equal to the bond’s duration.
Duration is also often interpreted as the percentage change in a bond’s price for a 1% change in its yield to maturity (YTM). So, for instance, the price of a bond with a 10-year duration would change by 10%.
Duration can be estimated by the following equation:
| Duration Approximation Formula | |
|---|---|
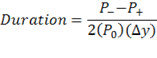 | P0 = Bond price. P- = Bond price when interest rate is incremented. P+ = Bond price when interest rate is decremented. ∆y = change in interest rate in decimal form. |
The interest rate is shocked up and down by a specific amount to obtain the new bond prices. Note that even if the interest rates are shocked by an amount different from 1%, duration is still interpreted as the percentage change in bond price for a 1% change in the YTM.
Macaulay Duration
It was Frederick Macaulay who developed the concept of duration, equating it to the average time to maturity or the time required to receive half of the present value, discounted by the bond’s yield to maturity, of the bond’s cash flow. The Macaulay duration is calculated by 1st calculating the weighted average of each cash flow at time t by the following formula:
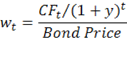 | wt = weighted average of cash flow at time t. CFt = Cash flow at time t. y = yield to maturity |
Then these weighted averages are summed:
| Macaulay Duration Formula | |
|---|---|
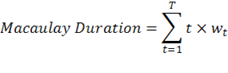 | T = number of cash flow periods. |
Hence, the Macaulay duration measures the effective maturity of a bond, and can also be used to calculate the average maturity of a portfolio of fixed-income securities.
Modified Duration
Modified duration is a modification of the Macaulay duration to estimate interest rate risk, calculating the change in a bond’s price to a change in its yield to maturity by the following formula:
| Modified Duration Formula | |
|---|---|
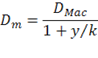 | Dm = Modified Duration DMac = Macaulay Duration y = yield to maturity k = number of payments per year |
The modified duration formula is valid only when the change in yield will not alter the cash flow of the bond, such as may occur, for instance, if the price change for a callable bond increases the likelihood that it will be called.
It is also only valid for small changes in yield, because duration itself changes as the yield changes. It is a 1st derivative of the price-yield curve, which is a line tangent to the curve at the current price-yield point.
| Duration and Modified Duration Formulas for Bonds using Microsoft Excel |
|---|
Duration = DURATION(settlement,maturity, Modified Duration = MDURATION(settlement,maturity,
|
1. Example—Calculating Modified Duration using Microsoft Excel
Calculate the duration and modified duration of a 10-year bond paying a coupon rate of 6%, a yield to maturity of 8%, and with a settlement date of 1/1/2008 and maturity date of 12/31/2017.
Duration = DURATION("1/1/2008","12/31/
Modified duration = MDURATION("1/1/2008","12/31/
Note that modified duration is always slightly less than duration, since the modified duration is the duration divided by 1 plus the yield per payment period.
Convexity adds a term to the modified duration, making it more precise, by accounting for the change in duration as the yield changes—hence, convexity is the 2nd derivative of the price-yield curve at the current price-yield point.
Although duration itself can never be negative, convexity can make it negative, since there are some securities, such as some mortgage-backed securities that exhibit negative convexity, meaning that the bond changes in price in the same direction as the yield changes.
Effective Duration for Option-Embedded Bonds
Because duration depends on the weighted averages of the present value of the bond’s cash flows, a simple calculation for duration is not valid if the change in yield could result in a change of cash flow. Valuation models must be used in calculating new prices for changes in yield when the cash flow is modified by options. The effective duration (aka option-adjusted duration) is the change in bond prices per change in yield when the change in yield can cause different cash flows. For instance, for a callable bond, the bond will not rise above the call price when interest rates decline because the issuer can call the bond back for the call price, and will probably do so if rates drop.
Because cash flows can change, the effective duration of an option-embedded bond is defined as the change in bond price per change in the market interest rate:
| Effective Duration Formula | |
|---|---|
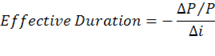 | ∆i = interest rate differential ∆P = Bond price at i + ∆i – bond price at i - ∆i. |
Note that i is the change in the term structure of interest rates and not the yield to maturity for the bond, because YTM is not valid for an option-embedded bond when the future cash flows are uncertain.
Duration Formulas for Specific Bonds and Annuities
There are several formulas for calculating the duration of specific bonds that are simpler than the above general formula.
The formula for the duration of a coupon bond is the following:
| Duration Formula for Coupon Bond | |
|---|---|
 | y = yield to maturity c = coupon interest rate in decimal formT = years till maturity |
If the coupon bond is selling for par value, then the above formula can be simplified:
| Duration Formula for Coupon Bond Selling for Face Value | |
|---|---|
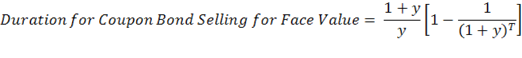 | y = yield to maturity T = years till maturity |
The duration of a fixed annuity for a specified number of payments T and yield per payment y can be calculated with the following formula:
| Fixed Annuity Duration Formula | |
|---|---|
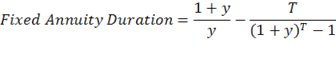 | y = yield to maturity T = years till maturity |
A perpetuity is a bond that does not have a maturity date, but pays interest indefinitely. Although the series of payments is infinite, the duration is finite, usually less than 15 years. The formula for the duration of a perpetuity is especially simple, since there is no principal repayment:
| Perpetuity Duration Formula | |
|---|---|
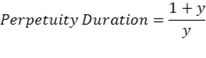 | y = yield to maturity |
Portfolio Duration
Duration is an effective analytic tool for the portfolio management of fixed-income securities because it provides an average maturity for the portfolio, which, in turn, provides a measure of interest rate risk to the portfolio.
The duration for a bond portfolio is equal to the weighted average of the duration for each type of bond in the portfolio:
Portfolio Duration = w1D1 + w2D2 + … + wKDK
- wi = market value of bond i / market value of portfolio
- Di = duration of bond i
- K = number of bonds in portfolio
To better measure the interest rate exposure of a portfolio, it is better to measure the contribution of the issue or sector duration to the portfolio duration rather than just measuring the market value of that issue or sector to the value of the portfolio:
Portfolio Duration Contribution = Weight of Issue in Portfolio x Duration of Issue
Convexity
Duration is only an approximation of the change in bond price. For small changes in yield, it is very accurate, but for larger changes in yield, it always underestimates the resulting bond prices for non-callable, option-free bonds. This is because duration is a tangent line to the price-yield curve at the calculated point, and the difference between the duration tangent line and the price-yield curve increases as the yield moves farther away in either direction from the point of tangency.
Convexity is the rate that the duration changes along the price-yield curve, and, thus, is the 1st derivative to the equation for the duration and the 2nd derivative to the equation for the price-yield function, and is calculated by the following equation:
| Convexity Formula | |
|---|---|
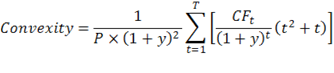 | P = Bond price. y = Yield to maturity in decimal form. T = Maturity in years. CFt=Cash flow at time t. |
The equation for duration can be improved by adding the convexity term:
| Calculating the Change in Bond Prices with Interest Rates Using Duration + Convexity Adjustment | |
|---|---|
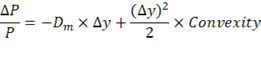 | ∆y = yield change ∆P = Bond price change |
Convexity can also be estimated with a simpler formula, similar to the approximation formula for duration:
| 1. Convexity Approximation Formula | ||
|---|---|---|
| Convexity = | P+ + P- - 2P0 ───────────── 2 x P0(Δy)2 | P0 = Bond price. P- = Bond price when interest rate is incremented. P+ = Bond price when interest rate is decremented. ∆y = change in interest rate in decimal form. |
Note, however, that this convexity approximation formula must be used with this convexity adjustment formula, then added to the duration adjustment:
| 1. Convexity Adjustment Formula | ||
|---|---|---|
| Convexity Adjustment = Convexity x 100 x (Δy)2 | ∆y = change in interest rate in decimal form. | |
Hence:
| Bond Price Change Formula |
|---|
| Bond Price Change = Duration x Yield Change + Convexity Adjustment |
Important Note! The convexity can actually have several values depending on the convexity adjustment formula used. Many calculators on the Internet calculate convexity according to the following formula:
| 2. Convexity Approximation Formula | ||
|---|---|---|
| Convexity = | P+ + P- - 2P0 ───────────── P0(Δy)2 | P0 = Bond price. P- = Bond price when interest rate is incremented. P+ = Bond price when interest rate is decremented. ∆y = change in interest rate in decimal form. |
Note that this formula yields double the convexity as the Convexity Approximation Formula #1. However, if this equation is used, then the convexity adjustment formula becomes:
| 2. Convexity Adjustment Formula | |
|---|---|
| Convexity Adjustment = Convexity/2 x 100 x (Δy)2 | ∆y = change in interest rate in decimal form. |
As you can see in the Convexity Adjustment Formula #2 that the convexity is divided by 2, so using the Formula #2's together yields the same result as using the Formula #1's together.
To add further to the confusion, sometimes both convexity measure formulas are calculated by multiplying the denominator by 100, in which case, the corresponding convexity adjustment formulas are multiplied by 10,000 instead of just 100! Just keep in mind that convexity values as calculated by various calculators on the Internet can yield results that differ by a factor of 100. They can all be correct if the correct convexity adjustment formula is used!
Convexity is usually a positive term regardless of whether the yield is rising or falling, hence, it is positive convexity. However, sometimes the convexity term is negative, such as occurs when a callable bond is nearing its call price. Below the call price, the price-yield curve follows the same positive convexity as an option-free bond, but as the yield falls and the bond price rises to near the call price, the positive convexity becomes negative convexity, where the bond price is limited at the top by the call price. Hence, similar to the terms for modified and effective duration, there is also modified convexity, which is the measured convexity when there is no expected change in future cash flows, and effective convexity, which is the convexity measure for a bond for which future cash flows are expected to change.
Price Value of a Basis Point
Sometimes the volatility of bond prices to interest rates is calculated as the absolute value of the change in price when the interest rate changes by 1 basis point (0.01%), which is called, aptly enough, the price value of a basis point (PVBP), or the dollar value of a 01 (DV01).
PVBP = |initial price – price if yield changes by 1 basis point|
(Math note: the expression |x| denotes the absolute value of x.)
Although bond prices increase more when yields decline than decrease when yields increase, a change in yield of 1 basis point is considered so small that the difference is negligible. Since duration is the approximate change in bond price for a 100 basis point change in yield, the price value of a basis point is 1% of the duration percentage.
For instance, in the example of above, the duration for the bond was found to be 7.45%. Hence, the PVBP is equal to:
PVBP = Duration x 1% = 7.45% x 0.01 = 0.0745 x 0.01 = .0745%
So a bond selling for par would change by:
Price Change = 100 x 0.0745% = 100 x 0.000745 = $0.0745
Hence, a bond with a par value of $1,000 would change in price by $0.75 (rounded) when the yield changes by 1 basis point.
Yield Volatility (Interest Rate Volatility)
Duration gives an estimate of the interest rate risk of a particular bond by relating the change in price to the change in yield, but neither duration nor convexity gives a complete picture of interest rate risk because some bonds change in yield, and therefore price, more than other bonds, for a given coupon rate and current yield, when the prevailing rates change, primarily due to changes in the perceived probability of default risk.
For instance, U.S. Treasuries generally have lower coupon rates and current yields than corporate bonds of similar maturities because of the difference in default risk. Therefore, U.S. Treasuries should have higher durations than corporate bonds, and, therefore, change in price more when market interest rates change. However, changes in perception of the risk of default may also change, blunting or augmenting what duration would predict.
For instance, during the recent subprime mortgage crisis, many bonds were perceived to be more risky than investors realized, even those that had received top ratings from the credit rating agencies, and so, many securities, especially those based on subprime mortgages, lost value, greatly increasing their yields, while yields on Treasuries declined as the demand for these securities, which are considered to be free of default risk, increased in price caused, not by the decline in market interest rates, but by the flight to quality—selling risky securities to buy securities with little or no default risk. The flight to quality is augmented by the fact that laws and regulations require that pension funds and other funds that are held for the benefit of others in a fiduciary capacity be invested in investment grade securities. So when investment ratings decline for a large number of securities to below investment grade, managers of funds held in trust must sell the riskier securities and buy securities that are likely to retain an investment grade rating or be free of default risk—in most cases, U.S. Treasuries.
Therefore, yield volatility, and therefore, interest rate risk, is greater for securities with more default risk, even if their durations are the same.
Duration and Maturity
This article provides a brief introduction to the duration measure for bonds. The duration measure for bonds is a invention that allows bonds of different maturities and coupon rates to be compared directly.
Everyone knows that the maturity of a bond is the amount of time left until it matures. Most people also know that the price of a bond swings more violently with interest rates the longer the maturity of the bond is. What many people don't know is that maturity is actually not that great a measure of the lifetime of a bond. Enter duration.
The reason why maturity isn't that great a measure is that it does not account for the differences in bond coupons. A 10-year bond with a 5% coupon will be more sensitive to interest rate changes than a 10-year bond with an 8% coupon. A 5-year zero-coupon bond may well be more sensitive than a 7-year 6% bond, and so forth.
Faced with the inadequacy of maturity, the investment gurus came up with a measure that takes both maturity and coupon rate into account in order to make apples-to-apples comparisons. The measure is called duration.
There are different ways to compute duration. I will use one of the common definitions, namely:
Duration is a weighted average of the times that interest payments and the final return of principal are received. The weights are the amounts of the payments discounted by the yield-to-maturity of the bond.The final sentence may be alternatively stated:
The weights are the present values of the payments, using the bond's yield-to-maturity as the discount rate.
Duration gives one an immediate rule of thumb -- the percentage change in the price of a bond is the duration multiplied by the change in interest rates. So if a bond has a duration of 10 years and intermediate-term interest rates fall from 8% to 6% (a drop of 2 percentage points), the bond's price will rise by approximately 20%.
In the examples and formulas that follow, I make the simplifying assumptions that:
- Interest payments occur annually (they actually occur every 6 months for most bonds).
- The final interest payment occurs on the date of maturity.
- It is always one year from now to the first interest payment.
It turns out that (especially for intermediate- and long-term bonds) these simplifications don't affect the final numbers that much -- duration is well less than a year different from its "true" value, even for something as short as a duration of 5 years.
Example 1:
Bond has a $10,000 face value and a 7% coupon. The yield-to-maturity
(YTM) is 5% and it matures in 5 years. The bond thus pays $700 a year
from now, $700 in 2 years, $700 in 3 years, $700 in 4 years, $700 in 5
years and the $10,000 return of principal also in 5 years.
As you may recall, to compute the weighted average of a set of numbers, you multiply the numbers by the weights and add those products up. You then add all the weights up and divide the former by the latter. In this case the weights are $700/1.05, $700/1.05^2, $700/1.05^3, $700/1.05^4, $700/1.05^5, and $10,000/1.05^5, or $666.67, $634.92, $604.69, $575.89, $548.47, and $7,835.26. The numbers being average are the times the payments are received, or 1 year, 2 years, 3 years, 4 years, 5 years, and 5 years. So the duration is:
1*$667.67 + 2*$634.92 + 3*$604.69 + 4*$575.89 + 5*$548.47 + 5*$7,835.26 D = ------------------------------D = 4.37 years------------------------------ ----------- $667.67 + $634.92 + $604.69 + $575.89 + $548.47 + $7,835.26
Example 2:
Bond has a face value of $P, coupon of c, YTM of y, maturity of M years.
1Pc/(1+y) + 2Pc/(1+y)^2 + 3Pc/(1+y)^3 + ... + MPc/(1+y)^M + MP/(1+y)^M D = ------------------------------We can use summations to condense this equation:------------------------------ --------------- Pc/(1+y) + Pc/(1+y)^2 + Pc/(1+y)^3 + ... + Pc/(1+y)^M + P/(1+y)^M
M
Pc*Sum i/(1+y)^i + MP/(1+y)^M
i=1
D = ------------------------------
M
Pc*Sum 1/(1+y)^i + P/(1+y)^M
i=1
We can cancel out the face value of P, leaving a function only of coupon,
YTM and time to maturity:
M
c*Sum i/(1+y)^i + M/(1+y)^M
i=1
D = -----------------------------------
M
c*Sum 1/(1+y)^i + 1/(1+y)^M
i=1
It is trivial to write a computer program to carry out the
calculation. And those of you who remember how to find a closed-form
expression for Sum{i=1 to M}(x^i) and Sum{i=1 to M}(ix^i) can grind
through the resulting algebra and get a closed-form expression for
duration that doesn't involve summation loops :-)
Note that any bond with a non-zero coupon will have a duration shorter than its maturity. For example, a 30 year bond with a 7% coupon and a 6% YTM has a duration of only 14.2 years. However, a zero will have a duration exactly equal to its maturity. A 30 year zero has a duration of 30 years. Keeping in mind the rule of thumb that the percentage price change of a bond roughly equals its duration times the change in interest rates, one can begin to see how much more volatile a zero can be than a coupon bond.

